系统模型
给定系统模型
\begin{align}
\boldsymbol{y}=g(\boldsymbol{x})
\end{align}
其中$\boldsymbol{x}\in \mathbb{R}^M$是目标信号,其随机性由先验概率$p(\boldsymbol{x})$刻画;$\boldsymbol{y}\in \mathbb{R}^N$是观测信号;函数$g(\cdot)$表示从$N$维空间到$M$维空间的映射,即$g(\cdot):\mathbb{R}^N\rightarrow \mathbb{R}^M$。在信号重构理论的研究对象中,映射$g(\cdot)$以及先验概率$p(\boldsymbol{x})$均给定,我们需要从观测信号$\boldsymbol{y}$中恢复出目标信号$\boldsymbol{x}$来。映射函数$g(\cdot)$可以是线性的,如线性高斯模型$g(\boldsymbol{x})=\boldsymbol{Hx}+\boldsymbol{w}$,也可以是非线性函数,如ADC量化模型$g(\boldsymbol{x})=Q(\boldsymbol{Hx}+\boldsymbol{w})$,其中$Q(\cdot)$表示均匀量化函数。
贝叶斯估计理论是众多信号重构算法中的一类算法。贝叶斯估计器被定义为使得如下贝叶斯风险函数最小
\begin{align}
\hat{\boldsymbol{x} }_{\text{Bayse} }
&=\underset{\hat{\boldsymbol{x} } }{\arg \min}\ \mathbb{E}_{\boldsymbol{x},\boldsymbol{y} }\left[\mathcal{C}(\boldsymbol{\epsilon})\right]\\
&=\underset{\hat{\boldsymbol{x} } }{\arg \min} \int_{\boldsymbol{y} }\left[\int_{\boldsymbol{x} }\mathcal{C}(\boldsymbol{\epsilon})p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}\right]p(\boldsymbol{y})\text{d}\boldsymbol{y}\\
&=\underset{\hat{\boldsymbol{x} } }{\arg \min} \int_{\boldsymbol{x} }\mathcal{C}(\boldsymbol{\epsilon})p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
其中$\mathcal{C}(\boldsymbol{\epsilon})$表示代价函数,$\boldsymbol{\epsilon}=\hat{\boldsymbol{x} }-\boldsymbol{x}$。 为了简化符号,定义
\begin{align}
g(\epsilon)\overset{\triangle}{=}\int_{\boldsymbol{x} }\mathcal{C}(\epsilon) p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
换言之,贝叶斯估计器是通过最小化$g(\boldsymbol{\epsilon})$得到。为了得到贝叶斯估计器的具体表达式,我们需要进一步确定代价函数的具体形式。特别需要注意的是,代价函数的选择应该数学上尽量简单出发。满足此要求的代价函数,如图所示,有二次误差型(quadratic error)、成功-失败型(hit-or-miss error)、绝对误差型(absolute error)。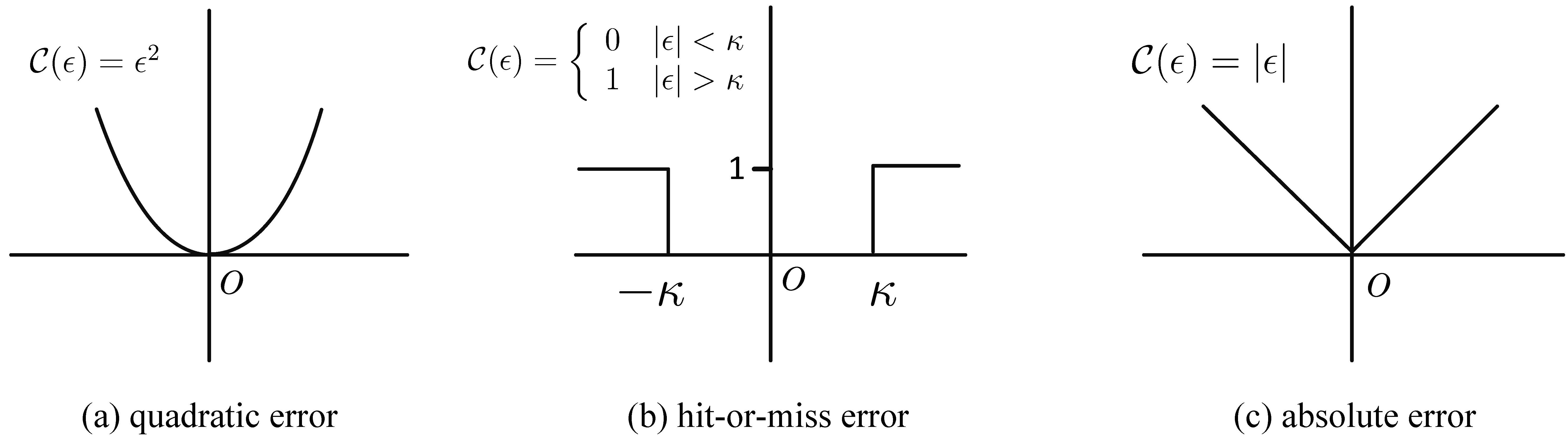
最小均误差估计器
当选择代价函数为二次误差型函数时,有
\begin{align}
g(\boldsymbol{\epsilon})=\int_{\boldsymbol{x} } |\hat{\boldsymbol{x} }-\boldsymbol{x}|^2 p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
上式求$\hat{\boldsymbol{x} }$求偏导,并设偏导为0,有
\begin{align}
\int (\hat{\boldsymbol{x} }-\boldsymbol{x}) p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}=0
\end{align}
整理为
\begin{align}
\hat{\boldsymbol{x} }=\mathbb{E}\left[\boldsymbol{x}|\boldsymbol{y}\right]=\int_{\boldsymbol{x} }\boldsymbol{x} p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
由于该估计器使得均方误差最小,因此被称之为最小均方误差估计。此外,该估计器的表达形式为后验概率的均值,因此也被称为后验均值估计。
最大后验概率估计器
当选择代价函数为“成功-失败”型代价函数(图b)时,有
\begin{align}
g(\boldsymbol{\epsilon})
&=\lim_{\kappa\rightarrow 0} \left[
\int_{\hat{\boldsymbol{x} }+\kappa}^{+\infty}p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}+\int_{-\infty}^{\hat{\boldsymbol{x} }-\kappa}p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\right]\\
&=1-\lim_{\kappa\rightarrow 0}\int_{\hat{\boldsymbol{x} }-\kappa}^{\hat{\boldsymbol{x} }+\kappa}p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
为了使得$g(\boldsymbol{\epsilon})$最小,需使得$\lim_{\kappa\rightarrow 0}\int_{\hat{\boldsymbol{x} }-\kappa}^{\hat{\boldsymbol{x} }+\kappa}p(\boldsymbol{x}|\boldsymbol{y})$最大,因此选择后验概率的最大值点作为估计器。由于该估计器选择后验概率的最大值点作为估计器,因此被称为最大后验概率估计,即
\begin{align}
\hat{\boldsymbol{x} }=\underset{\boldsymbol{x} }{\arg \max} \ p(\boldsymbol{x}|\boldsymbol{y})
\end{align}
若选择绝对误差型误差函数时,此时
\begin{align}
g(\boldsymbol{\epsilon})
&=\int |\boldsymbol{x}-\hat{\boldsymbol{x} }| p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}\\
&=\int_{\hat{\boldsymbol{x} } }^{+\infty} (\boldsymbol{x}-\hat{\boldsymbol{x} }) p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}+\int_{-\infty}^{\hat{\boldsymbol{x} } } (\hat{\boldsymbol{x} }-\boldsymbol{x})p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
上式对$\hat{\boldsymbol{x} }$求偏导,并令其为0,得到
\begin{align}
\int_{-\infty}^{\hat{\boldsymbol{x} } }p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}=\int_{\hat{\boldsymbol{x} } }^{+\infty}p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
此时估计器$\hat{\boldsymbol{x} }$为后验概率$p(\boldsymbol{x}|\boldsymbol{y})$的中值点,即$\text{Pr}(\boldsymbol{x}\leq \hat{\boldsymbol{x} })=\frac{1}{2}$。
通常来说,如下图所示后验概率的均值点、最大值点、中值点各不一样。特别地,若后验概率为高斯分布时,三点重合。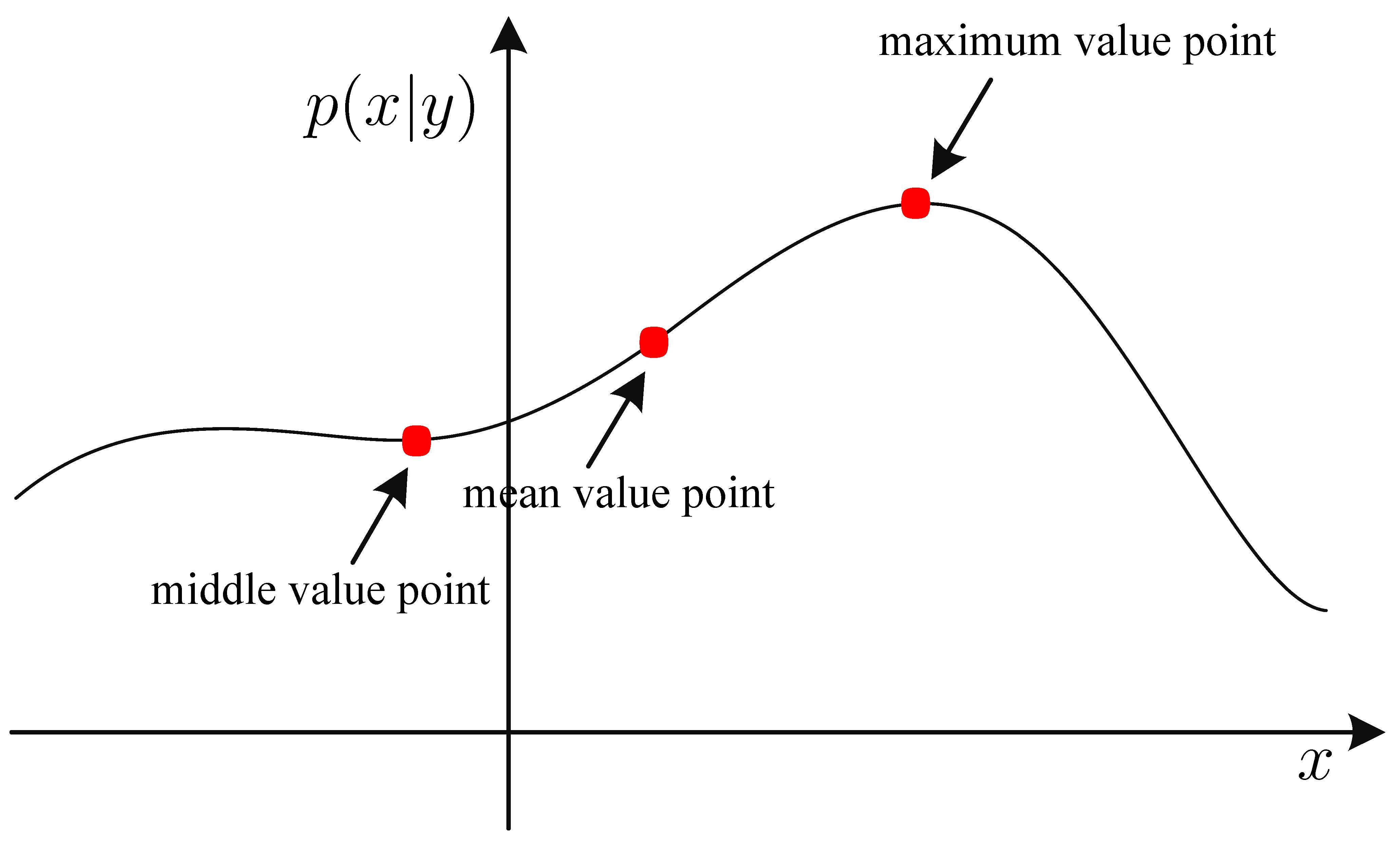
事实上,后验概率的中值点通常难以得到,除了某些特殊分布,如高斯分布,因此,常用的贝叶斯估计器主要指最小均方误差估计和最大后验概率估计。