引言
前馈神经网络参数的更新,其难点在于计算误差函数的梯度。为此,我们的目标是寻找一种计算前馈神经网络的误差函数$E(\boldsymbol{w})$的梯度的一种高效方法。我们会看到,可以使用局部信息传递的思想完成这一点。在局部信息传递的思想中,信息在神经网络中交替地向前、向后传播。这种方法被称为误差反向传播(back propagation,BP)。
值得注意的是,在神经网络的文献中,“反向传播”这个术语用于指代许多不同的事物。例如,前馈神经网络有时被称为反向传播网络。反向传播这个术语还用于描述将梯度下降法应用于平方和误差函数的多层感知器的训练过程。大部分网络的训练过程包含两个阶段
- 第一阶段:计算误差函数关于权值的导数,反向传播方法的一个重要贡献就是提供了计算这些导数的一个高效方法。由于正式这个阶段,误差通过网络进行反向传播,因此我们用反向传播特指导数计算的过程。
- 第二阶段:根据所计算的导数调整权值。这一步涉及到梯度下降。
这里,我们通过单隐层的例子,介绍误差反向传播算法的过程。理解好了单隐层,可以很好得扩展到前馈神经网络(多层感知机)。
Example (Single Hidden layer)
给定训练集$\mathcal{D}=\left\{(\boldsymbol{x}_i,\boldsymbol{y}_i)\right\}_{i=1}^m,\boldsymbol{x}_i\in \mathbb{R}^d,\boldsymbol{y}_i\in \mathbb{R}^{\ell}$,我们通过单隐层的例子进行介,假设隐含层和输出层使用的激活函数均为Sigmoid函数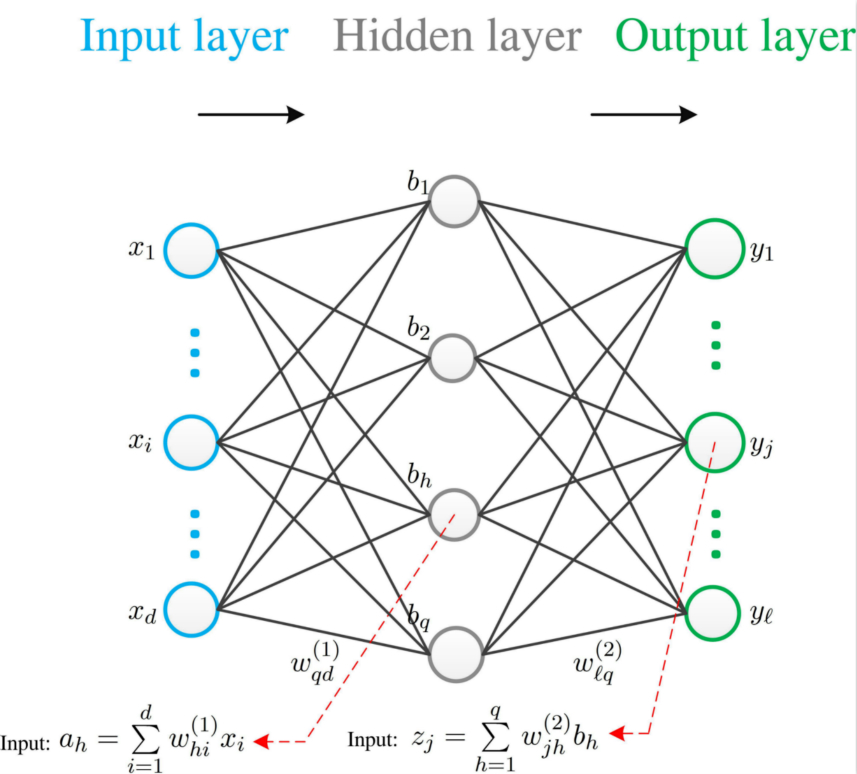
$\underline{\text{Step 1} }$: 对于数据$(\boldsymbol{x}_k,\boldsymbol{y}_k)$,假定神经网络的输出为$\hat{\boldsymbol{y} }_k=(\hat{y}_1^k,\cdots,\hat{y}_l^k)$,计算误差$E_k$,即
\begin{align}
\hat{y}_j^k=f(z_j-\theta^{(2)}_j)
\end{align}
则,网络的均方误差为
\begin{align}
E_k=\frac{1}{2}\sum_{j=1}^l (\hat{y}_l^k-y_j^k)^2
\end{align}
$\underline{\text{Step 2} }:$ 计算“第二层”权重$w_{jh}^{(2)},(j=1,\cdots,\ell; h=1,\cdots,q)$。反向传播算法中参数的更新均采用如下形式
\begin{align}
v\leftarrow v+\triangle v
\end{align}
因此“第二层”权重的更新步长为
\begin{align}
\triangle w_{jh}^{(2)}
&=-\eta \frac{\partial E_k}{\partial w_{jh}^{(2)} }\\
&=-\eta\frac{\partial E_k}{\partial \hat{y}_j^k}\frac{\partial \hat{y}_j^k}{\partial z_j}\frac{\partial z_j}{\partial w_{jh}^{(2)} }
\end{align}
其中$\frac{\partial z_j}{\partial w_{jh} }=b_h$,另外,根据Sigmoid函数的特性
\begin{align}
f’(x)=f(x)(1-f(x))
\end{align}
有
\begin{align}
g_j
&\overset{\triangle}{=}-\frac{\partial E_k}{\partial \hat{y}_j^k}\frac{\partial \hat{y}_j^k}{\partial z_j}\\
&=-(\hat{y}_j^k-y_j^k)f’(z_j-w_0^{(2)})\\
&=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k)
\end{align}
因此,我们可以得到
\begin{align}
\triangle w_{jh}=\eta g_jb_h
\end{align}
进而更新
\begin{align}
w_{jh}^{(2)}\leftarrow w_{jh}^{(2)}+\eta g_jb_h
\end{align}
$\underline{\text{Step 3} }:$ 计算“第二层”偏置$\theta_{j}^{(2)}$。
\begin{align}
\triangle \theta_j^{(2)}
&=-\eta \frac{\partial E_k}{\partial \theta_j^{(2)} }\\
&=-\eta\frac{\partial E_k}{\partial \hat{y}_j^k}\frac{\partial \hat{y}_j^k}{\partial \theta_j^{(2)} }\\
&=\eta g_j
\end{align}
进而更新
\begin{align}
\theta_j^{(2)}\leftarrow \theta_j^{(2)}+\eta g_j
\end{align}
$\underline{\text{Step 4} }:$按照前两步的方式,计算“第一层”权重$w_{hi}^{(1)},( h=1,\cdots,q;i=1,\cdots,d)$和偏置
\begin{align}
\triangle w_{hi}^{(1)}&=\eta e_hx_i\\
\triangle \theta_h^{(1)}&=-\eta e_h
\end{align}
其中
\begin{align}
e_h
&=-\frac{\partial E_k}{\partial b_h}\frac{\partial b_h}{\partial a_h}\\
&=-\sum_{j=1}^{\ell}\frac{\partial E_k}{\partial z_j} \frac{\partial z_j}{\partial b_h}f’(a_h-\theta_h^{(1)})\\
&=\sum_{j=1}^{\ell}w_{jh}g_jf’(a_h-\theta_h^{(1)})\\
&=b_h(1-b_h)\sum_{j=1}^{\ell}w_{jh}g_j
\end{align}
进而更新
\begin{align}
w_{hi}^{(1)}&\leftarrow w_{hi}^{(1)}+\eta e_hx_i\\
\theta_h^{(1)}&\leftarrow \theta_h^{(1)}-\eta e_h
\end{align}
$\underline{\text{Step 5} }:$ $\longrightarrow $ ${\text{Step 1} }$,直到终止条件。
Remarks
- 误差$E_k$更新,是前向进行的
- 权重的更新,是逆向传播。