对于线性高斯模型
\begin{align}
\boldsymbol{y}=\boldsymbol{Hx}+\boldsymbol{w}
\end{align}
其中$\boldsymbol{x}\in \mathbb{R}^N$为待估计变量,其概率密度为$p(\boldsymbol{x})$。$\boldsymbol{w}$是高斯白噪声,即$\boldsymbol{w}\sim \mathcal{N}(\boldsymbol{w}|\boldsymbol{a},\boldsymbol{C}_{\boldsymbol{w} })$。信号估计的目标是根据已知的模型信息,从观测向量$\boldsymbol{y}\in \mathbb{R}^M$中恢复出原始信号$\boldsymbol{x}$。为了得到确定解,一般$\boldsymbol{y}$的维度大于$\boldsymbol{x}$的维度,即模型为超定方程组。
最小二乘法 (Least Square, LS)
$\boldsymbol{x}$的最小二乘估计,通过最小化如下损失函数得到
\begin{align}
J=||\boldsymbol{y}-\boldsymbol{Hx}||^2
\end{align}
由于该损失函数是凸函数,因此我们通过计算损失函数对$\boldsymbol{x}$的导数
\begin{align}
\frac{\partial J}{\partial \boldsymbol{x} }=-2\boldsymbol{H}^T\boldsymbol{y}+2\boldsymbol{H}^T\boldsymbol{H}\boldsymbol{x}
\end{align}
并令导数为零,得到该模型的最小二乘估计
\begin{align}
\hat{\boldsymbol{x} }_{\text{LS} }=(\boldsymbol{H}^T\boldsymbol{H})^{-1}\boldsymbol{H}^T\boldsymbol{y}
\end{align}
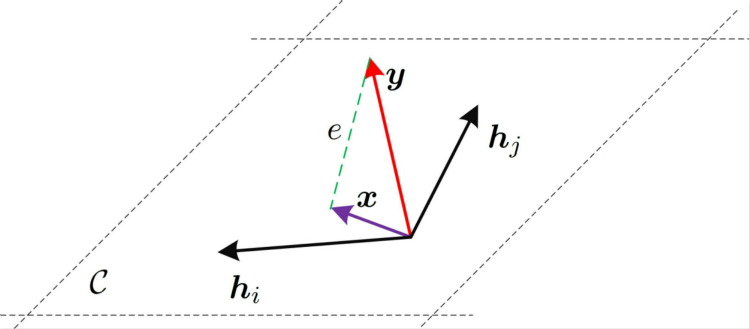
几何解释: 如图所示,由于$\boldsymbol{H}$所构成的超平面用$\mathcal{C}$表示,最小化$J=||\boldsymbol{y}-\boldsymbol{Hx}||^2$所描述的是,找到$\boldsymbol{y}$在超平面$\mathcal{C}$上的正交投影。
Remarks: 最小二乘的优势在于算法结构简单,其缺陷在于,由于忽略了噪声的存在,因此当噪声很大的时候,其估计性能极差。
最大似然估计(Maximum likelihood, ML)
似然函数的定义(摘自Wiki Pedia):
In frequentist inference, a likelihood function (often simply the likelihood) is a function of the parameters of a statistical model, given specific observed data. Likelihood functions play a key role in frequentist inference, especially methods of estimating a parameter from a set of statistics. In informal contexts, “likelihood” is often used as a synonym for “probability”. In mathematical statistics, the two terms have different meanings. Probability in this mathematical context describes the plausibility of a random outcome, given a model parameter value, without reference to any observed data. Likelihood describes the plausibility of a model parameter value, given specific observed data.
在概率推论中,一个似然函数(简称似然)是给定明确的观测数据,关于一个统计模型的参数的函数。似然函数在概率推论中扮演着重要的角色,尤其是从一组统计数据中估计参数。在非正式的文献中,似然函数通常被认为是“概率”。在统计数学中,这两者有不同的含义。在数学文献中,概率描述的是给定模型参数值下一个随机输出的可能性,没有参考任何观测数据。似然函数描述的是给定具体观测数据,模型参数值得可能性。
Following Bayes’ Rule, the likelihood when seen as a conditional density can be multiplied by the prior probability density of the parameter and then normalized, to give a posterior probability density.
根据贝叶斯公式,似然函数被看作是条件概率,可以乘上先验概率然后归一化得到后验概率。
对于线性高斯模型$\boldsymbol{y}=\boldsymbol{Hx}+\boldsymbol{w}$,为了方便计算,这里我们设$\boldsymbol{w}\sim \mathcal{N}(\boldsymbol{0},\sigma^2\mathbf{I})$,则该模型的其似然函数为
\begin{align}
L(\boldsymbol{x})&=p(\boldsymbol{y}|\boldsymbol{x})=\mathcal{N}(\boldsymbol{y}|\boldsymbol{Hx},\sigma^2\mathbf{I})\\
&=(2\pi\sigma^2)^{-\frac{M}{2} }\exp \left(-\frac{1}{2\sigma^2}(\boldsymbol{y}-\boldsymbol{Hx})^T(\boldsymbol{y}-\boldsymbol{Hx})\right)
\end{align}
等式两边取对数,有
\begin{align}
\ell(\boldsymbol{x})=\ln L(\boldsymbol{x})=-\frac{1}{2\sigma^2}(\boldsymbol{y}-\boldsymbol{Hx})^T(\boldsymbol{y}-\boldsymbol{Hx})-\frac{M}{2}\ln (2\pi\sigma^2)
\end{align}
计算对数似然函数关于$\boldsymbol{x}$的偏导数,有
\begin{align}
\frac{\partial \ell(\boldsymbol{x})}{\partial \boldsymbol{x} }=-\frac{1}{2\sigma^2}(2\boldsymbol{H}^T\boldsymbol{y}-2\boldsymbol{H}^T\boldsymbol{H}\boldsymbol{x})=0 \ \Rightarrow \hat{\boldsymbol{x} }_{\text{ML} }=(\boldsymbol{H}^T\boldsymbol{H})^{-1}\boldsymbol{H}^T\boldsymbol{y}
\end{align}
因此,我们发现,线性高斯模型的最大似然解和最小二乘解一致。
最小均方误差估计(Minimum mean square error, MMSE)
定义如下贝叶斯均方误差(Bayesian mean square error, Bmse)
\begin{align}
\text{Bmse}(\hat{\boldsymbol{x} })=\mathbb{E}\left\{||\boldsymbol{x}-\hat{\boldsymbol{x} }||^2\right\}=\int ||\boldsymbol{x}-\hat{\boldsymbol{x} }||^2p(\boldsymbol{x},\boldsymbol{y})\text{d}\boldsymbol{x}\text{d}\boldsymbol{y}
\end{align}
最小均方误差估计量,即寻找使得贝叶斯均方误差最小的$\boldsymbol{x}$
\begin{align}
\hat{\boldsymbol{x} }
&=\underset{\boldsymbol{x} }{\arg \min} \int \left[\int ||\boldsymbol{x}-\hat{\boldsymbol{x} }||^2p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}\right]p(\boldsymbol{y})\text{d}\boldsymbol{y}\\
&=\underset{\boldsymbol{x} }{\arg \min}\int ||\boldsymbol{x}-\hat{\boldsymbol{x} }||^2p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
\end{align}
计算其导数
\begin{align}
\frac{\partial }{\partial \boldsymbol{x} }\int ||\boldsymbol{x}-\hat{\boldsymbol{x} }||^2p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}
&=2\int (\boldsymbol{x}-\hat{\boldsymbol{x} })p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}\\
&=2\int \boldsymbol{x}p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}-2\hat{\boldsymbol{x} }
\end{align}
注意$\hat{\boldsymbol{x} }$是关于$\boldsymbol{y}$的函数。令导数为0,有
\begin{align}
\hat{\boldsymbol{x} }_{\text{MMSE} }=\int \boldsymbol{x} p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}=\mathbb{E}\left[\boldsymbol{x}|\boldsymbol{y}\right]
\end{align}
Remarks:
- 最小均方误差估计器,被称为后验均值估计,也就是选取后验概率的均值作为$\boldsymbol{x}$的估计值。因此,最小均方误差估计器最为核心之处,在于计算后验概率$p(\boldsymbol{x}|\boldsymbol{y})$。根据贝叶斯公式
\begin{align}
p(\boldsymbol{x}|\boldsymbol{y})=\frac{p(\boldsymbol{x},\boldsymbol{y})}{p(\boldsymbol{y})}=\frac{p(\boldsymbol{y}|\boldsymbol{x})p(\boldsymbol{x})}{p(\boldsymbol{y})}
\end{align}
这里我们仅需要求$p(\boldsymbol{y}|\boldsymbol{x})p(\boldsymbol{x})$,而$p(\boldsymbol{y})$可以通过归一化来实现。
\begin{align}
\hat{\boldsymbol{x} }=\left[
\begin{matrix}
\hat{x}_1\\
\vdots\\
\hat{x}_N
\end{matrix}
\right]=\left[
\begin{matrix}
\int x_1p(x_1|\boldsymbol{y})\text{d}x_1\\
\vdots\\
\int x_1p(x_N|\boldsymbol{y})\text{d}x_N
\end{matrix}
\right]
\end{align}
因此,我们可以知道,最小均方误差真正的难点在于,求边缘后验概率
\begin{align}
p(x_i|\boldsymbol{y})=\int_{\boldsymbol{x}_{\backslash i} } p(\boldsymbol{x}|\boldsymbol{y})\text{d}\boldsymbol{x}_{\backslash i}
\end{align}
其中$\boldsymbol{x}_{\backslash i}$表示除了第$i$个元素外,$\boldsymbol{x}$中其余元素所构成的向量。- 最小均方误差估计器是贝叶斯最优的,因为,最小均方误差估计器选取使得贝叶斯均方误差最小的$\boldsymbol{x}$作为估计器。
- 当先验概率是高斯的时候,根据高斯相乘引理,我们可以写出线性高斯模型的MMSE估计器的解析表达式。
- 通常先验概率是非高斯的,此时,我们不能写出MMSE估计器的解析表达式。一种方法是,退而求其次,通过限制待估计量与观测值呈线性关系,即LMMSE估计器;另一种方法是通过因子图的角度出发,利用近似消息传递(approximate message passing, AMP)[1][2]类算法或者期望传播(Expectation propagation, EP)[3]类算法,来迭代得到估计量的MMSE解。注意,不管是AMP族算法还是EP族算法,其本质上是计算边缘后验概率。
线性最小均方误差估计 (Linear minmum mean square error, LMMSE)
线性最小均方误差估计,通过假设估计器的模型为$\boldsymbol{y}$的线性模型,并使得贝叶斯均方误差最小,来得到估计器的表达式
\begin{align}
\hat{\boldsymbol{x} }=\boldsymbol{A}\boldsymbol{y}+\boldsymbol{b}
\end{align}
为了得到$\boldsymbol{x}$的表达式,我们需要进一步确定$\boldsymbol{A}$和$\boldsymbol{b}$。定义如下贝叶斯均方误差(Bayesian mean square error, BMSE)
\begin{align}
\text{Bmse}(\hat{\boldsymbol{x} })=\mathbb{E}\left\{||\boldsymbol{x}-\hat{\boldsymbol{x} }||^2\right\}
\end{align}
这里的期望是对联合概率$p(\boldsymbol{x},\boldsymbol{y})$求。
$\underline{\text{Step 1} }$:为求$\hat{\boldsymbol{x} }=[\hat{x}_1,\cdots,\hat{x}_N]^T$,我们首先考虑一维的情况,即
\begin{align}
\hat{x}=\boldsymbol{a}^T\boldsymbol{y}+b
\end{align}
其对应的贝叶斯均方误差为
\begin{align}
\text{Bmse}(\hat{x })=\mathbb{E}\left\{(x-\hat{x})^2\right\}
\end{align}
其中期望对$p(x,\boldsymbol{y})$取。
$\underline{\text{Step 2} }$: 求$b$。计算贝叶斯均方误差对$b$的偏导,有
\begin{align}
\frac{\partial }{\partial b}\mathbb{E}\left\{(x-\boldsymbol{a}^T\boldsymbol{y}-b)^2\right\}=-2\mathbb{E}\left\{x-\boldsymbol{a}^T\boldsymbol{y}-b\right\}
\end{align}
令偏导为0,得到
\begin{align}
b=\mathbb{E}[x]-\boldsymbol{a}^T\mathbb{E}[\boldsymbol{y}]
\end{align}
$\underline{\text{Step 3} }$:计算$\boldsymbol{a}$。计算贝叶斯均方误差如下
\begin{align}
\text{Bmse}(\hat{x})
&=\mathbb{E}\left\{(x-\boldsymbol{a}^T\boldsymbol{y}-\mathbb{E}[x]+\boldsymbol{a}^T\mathbb{E}[\boldsymbol{y}])^2\right\}\\
&=\mathbb{E}\left\{\left[\boldsymbol{a}^T(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])-(x-\mathbb{E}[x])\right]^2\right\}\\
&=\mathbb{E}\left\{\boldsymbol{a}^T(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])^T\boldsymbol{a}\right\}-\mathbb{E}\left\{\boldsymbol{a}^T(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])(x-\mathbb{E}[x])\right\}\\
&\quad -\mathbb{E}\left\{(x-\mathbb{E}[x])(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])^T\boldsymbol{a}\right\}+\mathbb{E}\left\{(x-\mathbb{E}[x])^2\right\}\\
&=\boldsymbol{a}^T\boldsymbol{C}_{\boldsymbol{yy} }\boldsymbol{a}-\boldsymbol{a}^T\boldsymbol{C}_{\boldsymbol{y}x}-\boldsymbol{C}_{x\boldsymbol{y} }\boldsymbol{a}+C_{xx}
\end{align}
其中$\boldsymbol{C}_{\boldsymbol{yy} }$是$\boldsymbol{y}$的协方差矩阵,$\boldsymbol{C}_{x\boldsymbol{y} }$是$1\times N$的互协方差矢量,且$\boldsymbol{C}_{x\boldsymbol{y} }=\boldsymbol{C}_{\boldsymbol{y}x}^T$。$C_{xx}$是$x$的方差。计算贝叶斯均方误差对$\boldsymbol{a}$的偏导,并令偏导为0,有
\begin{align}
\frac{\partial \text{Bmse}(\hat{\boldsymbol{x} })}{\partial \boldsymbol{a} }=2\boldsymbol{C}_{\boldsymbol{yy} }\boldsymbol{a}-2\boldsymbol{C}_{\boldsymbol{y}x}=0 \quad \Rightarrow \boldsymbol{a}=C_{\boldsymbol{yy} }^{-1}\boldsymbol{C}_{\boldsymbol{y}x}
\end{align}
因此,得到
\begin{align}
\hat{x}
&=\boldsymbol{C}_{x\boldsymbol{y} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}\boldsymbol{y}+\mathbb{E}[x]-\boldsymbol{C}_{x\boldsymbol{y} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}\mathbb{E}[\boldsymbol{y}]\\
&=\boldsymbol{C}_{x\boldsymbol{y} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])+\mathbb{E}[x]
\end{align}
$\underline{\text{Step 4} }$:扩展到矢量$\hat{\boldsymbol{x} }$。
\begin{align}
\hat{\boldsymbol{x} }
&=\left[
\begin{matrix}
\mathbb{E}[x_1]\\
\mathbb{E}[x_2]\\
\vdots\\
\mathbb{E}[x_N]\\
\end{matrix}
\right]
+
\left[
\begin{matrix}
\boldsymbol{C}_{x_1\boldsymbol{y} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])\\
\boldsymbol{C}_{x_2\boldsymbol{y} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])\\
\vdots\\
\boldsymbol{C}_{x_N\boldsymbol{y} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])\\
\end{matrix}
\right]\\
&=\mathbb{E}[\boldsymbol{x}]+\boldsymbol{C}_{\boldsymbol{xy} }\boldsymbol{C}_{\boldsymbol{yy} }^{-1}(\boldsymbol{y}-\mathbb{E}[\boldsymbol{y}])
\end{align}
其中
\begin{align}
\boldsymbol{C}_{\boldsymbol{yy} }
&=\boldsymbol{H}\boldsymbol{C}_{\boldsymbol{xx} }\boldsymbol{H}^T+\boldsymbol{C}_{\boldsymbol{w} }\\
\boldsymbol{C}_{\boldsymbol{xy} }&=\boldsymbol{C}_{\boldsymbol{xx} }\boldsymbol{H}^T
\end{align}
因此
\begin{align}
\hat{\boldsymbol{x} }_{\text{LMMSE} }
&=\mathbb{E}[\boldsymbol{x}]+\boldsymbol{C}_{\boldsymbol{xx} }\boldsymbol{H}^T(\boldsymbol{H}\boldsymbol{C}_{\boldsymbol{xx} }\boldsymbol{H}^T+\boldsymbol{C}_{\boldsymbol{w} })^{-1}(\boldsymbol{y}-\boldsymbol{H}\mathbb{E}[\boldsymbol{x}])\\
&=\mathbb{E}[\boldsymbol{x}]+(\boldsymbol{C}_{\boldsymbol{xx} }^{-1}+\boldsymbol{H}^T\boldsymbol{C}_{\boldsymbol{w} }^{-1}\boldsymbol{H})^{-1}\boldsymbol{H}^T\boldsymbol{C}_{\boldsymbol{w} }^{-1}(\boldsymbol{y}-\boldsymbol{H}\mathbb{E}[\boldsymbol{x}])
\end{align}
Remarks:
- 通常我们所遇到的模型中,经过功率归一化后,$\boldsymbol{x}$的均值为0,方差为1,以及噪声方差为$\sigma^2$。因此,进一步将其LMMSE估计器简化为
\begin{align}
\hat{\boldsymbol{x} }_{\text{LMMSE} }=(\boldsymbol{H}^T\boldsymbol{H}+\sigma^2\mathbf{I})^{-1}\boldsymbol{H}^T\boldsymbol{y}
\end{align}
我们可以看到,相对于LS而言 $\left(\hat{\boldsymbol{x} }=(\boldsymbol{H}^T\boldsymbol{H})^{-1}\boldsymbol{H}^T\boldsymbol{y}\right)$,LMMSE加入了噪声修正项$\sigma^2\mathbf{I}$。- 对于简化后的LMMSE估计器模型$\hat{\boldsymbol{x} }=(\boldsymbol{H}^T\boldsymbol{H}+\sigma^2\mathbf{I})^{-1}\boldsymbol{H}^T\boldsymbol{y}$,我们可以将其视为,假设$\boldsymbol{x}\sim \mathcal{N}(\boldsymbol{x}|\boldsymbol{0},\mathbf{I})$的MMSE结果。证明如下
\begin{align}
p(\boldsymbol{x}|\boldsymbol{y})
&=\frac{p(\boldsymbol{x})p(\boldsymbol{y}|\boldsymbol{x})}{p(\boldsymbol{y})}\\
&\propto p(\boldsymbol{x})p(\boldsymbol{y}|\boldsymbol{x})
\end{align}
根据高斯相乘引理:
\begin{align}
p(\boldsymbol{x})p(\boldsymbol{y}|\boldsymbol{x})
&=\mathcal{N}(\boldsymbol{x}|\boldsymbol{0},\mathbf{I})\mathcal{N}(\boldsymbol{y}|\boldsymbol{Hx},\sigma^2\mathbf{I})\\
&\propto \mathcal{N}(\boldsymbol{x}|\boldsymbol{0},\mathbf{I})\mathcal{N}(\boldsymbol{x}|(\boldsymbol{H}^T\boldsymbol{H})^{-1}\boldsymbol{H}^T\boldsymbol{y},(\sigma^{-2}\boldsymbol{H}^T\boldsymbol{H})^{-1})\\
&\propto \mathcal{N}(\boldsymbol{x}|\boldsymbol{c},\boldsymbol{C})
\end{align}
其中
\begin{align}
\boldsymbol{C}&=(\sigma^{-2}\boldsymbol{H}^T\boldsymbol{H}+\mathbf{I})^{-1}\\
\boldsymbol{c}&=\boldsymbol{C}\cdot (\sigma^{-2}\boldsymbol{H}^T\boldsymbol{y})=(\boldsymbol{H}^T\boldsymbol{H}+\sigma^2\mathbf{I})^{-1}\boldsymbol{H}^T\boldsymbol{y}
\end{align}
由于$p(\boldsymbol{x}|\boldsymbol{y})$为高斯分布,因此,该模型的MMSE估计为其后验概率均值,即高斯的均值$\boldsymbol{c}=(\boldsymbol{H}^T\boldsymbol{H}+\sigma^2\mathbf{I})^{-1}\boldsymbol{H}^T\boldsymbol{y}$。我们可以看到,这与LMMSE解一致。
最大后验概率估计(Maximum a posterior, MAP)
最大后验概率估计,顾名思义,即选择后验概率最大值所处的$\boldsymbol{x}$作为估计器。
\begin{align}
\hat{\boldsymbol{x} }_{\text{MAP} }&=\underset{\boldsymbol{x} }{\arg \max} \ p(\boldsymbol{x}|\boldsymbol{y})\\
\end{align}
估计器$\hat{\boldsymbol{x} }$的元素表示为
\begin{align}
\hat{x}_i
&=\underset{x_i}{\arg \max} \left\{\max_{\boldsymbol{x}_{\backslash i} }\ p(\boldsymbol{x}|\boldsymbol{y})\right\}\\
&=\underset{x_i}{\arg \max} \left\{\max_{\boldsymbol{x}_{\backslash i} }\ \log p(\boldsymbol{x}|\boldsymbol{y})\right\}
\end{align}
Remarks: 特别地,当先验概率为高斯时候,利用高斯相乘引理,我们可以得到后验概率$p(\boldsymbol{x}|\boldsymbol{y})$是关于$\boldsymbol{x}$的高斯分布。此时,最大后验概率估计,为该高斯分布的均值点,相应地,这种情况下的MMSE估计和MAP估计是一致的。然而,通常情况下先验概率为非高斯的,这种情况下,我们可以利用AMP算法或者EP算法来迭代计算边缘后验概率。
References
[1] Donoho D L, Maleki A, Montanari A. How to design message passing algorithms for compressed sensing[J]. preprint, 2011.
[2] Meng X, Wu S, Kuang L, et al. Concise derivation of complex Bayesian approximate message passing via expectation propagation[J]. arXiv preprint arXiv:1509.08658, 2015.
[3] Minka T P. A family of algorithms for approximate Bayesian inference[D]. Massachusetts Institute of Technology, 2001.