引言　

学习傅里叶级数之后，我们得到一个结论，任何满足狄利克雷条件（Dirichlet Conditions）的周期信号$f(t)$可以分解为一串虚指数信号的线性加权和，即傅里叶级数。然而实际上，我们需要处理的信号大多为非周期信号。因此，要想对非周期信号进行频域分析，我们需要得到一个属于非周期信号的“傅里叶级数”。

在周期信号的分解中，我们选择信号的分解区间为$(a-T/2,a+T/2)$。当周期信号的周期$T\to\infty$时，周期信号就转换为非周期信号（周期$T\to\infty$），此时分解区间为$(-\infty,+\infty)$。

为了能够透彻整个傅里叶级数到傅里叶变换的过程，笔者先从黎曼积分讲起。然后再推导非周期信号的傅里叶变换公式。

黎曼积分

黎曼是德国数学家，数学分析大师，物理学家，被后人誉为定积分之父。对数学分析和微分几何做出了重要贡献，其中一些为广义相对论的发展铺平了道路。他的名字出现在黎曼ζ函数，黎曼积分，黎曼几何，黎曼引理，黎曼流形，黎曼映照定理，黎曼-希尔伯特问题，黎曼思路回环矩阵和黎曼曲面中。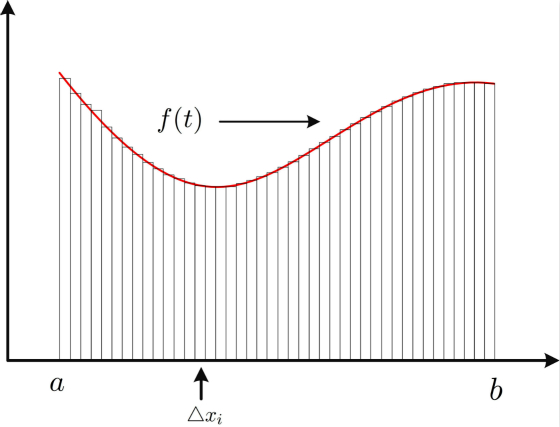

如何求函数$f(t)$在区间$[a,b]$上的面积呢？于是，黎曼想到将区间$[a,b]$划分为无数个子区间，设第$i$个区间的宽度为$\Delta x_i$，然后在该区间上任取一点$\xi_i\left(\xi_i\in [x_{i-1},x_i]\right)$，用$f(\xi_i)\triangle x_i$来表示该小柱条的面积。令$\lambda=\max \left\{\triangle x_i\right\}$，当$\lambda \to 0$时，函数$f(t)$在区间$[a,b]$上的面积可以表示为
\begin{align}
S=\lim_{\lambda\rightarrow 0} \sum_{i=1}^n f(\xi_i)\triangle x_i
\end{align}
通常采用等分切割处理，并选择区间最右端的函数值为小柱条的高，因此
\begin{align}
S=\lim_{n\rightarrow \infty} \sum_{i=1}^n f\left(a-\frac{b-a}{n}i\right)\frac{b-a}{n}
\end{align}
为了定义这个运算，黎曼翻阅书籍，由于该运算是极限求和，因此选取了求和单词Sum的首字母，并对其进行拉长也就是现在的积分符号$\int$。因此上式写为
\begin{align}
S=\int_a^b f(x)\text{d}x
\end{align}
心细的朋友应该会发现，即使$\lambda \to 0$，但还是存在误差，设每一个小柱条与该区间实际面积之差为$\triangle s_i$，那么总体误差为
\begin{align}
\triangle S=\sum_{i\rightarrow \infty}\triangle s_i
\end{align}
无穷个无穷小之和可能不为无穷小，因此式子的$S=\int_a^bf(x)\text{d}x$的成立还需证明$\Delta {S}\to 0$。这种工作一般需要数学家去完成，这里不进行扩展。至此，我们有了极限求和的思想。

再谈傅里叶级数

如图2所示，周期性方波信号，其周期为$T$，单周期内，方波持续时间为$2\tau $，讨论周期$T$对傅里叶级数$F_n$的影响。

该方波信号的傅里叶级数$F_n$
\begin{align}
F_n =\frac{\tau}{T}\text{Sa}\left({\frac{nw_0\tau}{2} }\right)
\end{align}
设$\tau=1/2$，讨论周期$T$对$F_n$的影响
【实验程序】

clear all
T=2;                  %信号周期
tau=1/2;              %方波持续时间
t=-20*pi:0.01:20*pi;  %包络显示范围
wo=2*pi/T;            %角频率
nwo=-20*pi:wo:20*pi;  %
Fn=(tau/T).*sinc(nwo*tau/(2*pi));  %傅里叶级数谱线
f=(tau/T).*sinc(t*tau/(2*pi));     %包络
stem(nwo,Fn)          %绘制傅里叶级数谱线
hold on
plot(t,f,'--r');      %绘制保罗谱线
hold on
title(strcat('T=',num2str(T)));
hold on

$T=2$，$\omega_o=\pi$
$T=4$，$\omega_o=\frac{\pi}{2}$
$T=8$，$\omega_o=\frac{\pi}{4}$
$T=16$，$\omega_o=\frac{\pi}{8}$
$T=32$，$\omega_o=\frac{\pi}{16}$

从上述实验可以看出，随着周期$T$的增大，频率谱线之间的间距逐渐减小，谱线的幅度逐渐减小。当$T\to \infty$时，频率谱线趋于连续谱线，谱线的幅度趋于0。然而，研究幅度为0的频率谱线是没有意义的，这又要如何处理呢？　　

从傅里叶级数到傅里叶变换

对于周期$T\to \infty$的周期信号$f(t)$，其傅里叶级数为
\begin{align}
F_n=\lim_{T\rightarrow \infty}\frac{1}{T} \int_T f(t)e^{-jnw_0t}\text{d}t
\end{align}
实际信号处理中，$f(t)$为有限长信号，因此$\int_T f(t)e^{-jnw_0t}\text{d}t$可以看做是一个有界常量，那么
\begin{align}
F_n=\lim_{T\rightarrow \infty} \frac{1}{T}\int_T f(t)e^{-jnw_0t}\text{d}t
\end{align}
就是一个无穷小量（无穷小乘以有界常量仍为无穷小）。因此，在等式两端同时乘以$T$，有
\begin{align}
TF_n=\lim_{T\rightarrow \infty}\int_T f(t)e^{-jnw_0t}\text{d}t
\end{align}
记$X(jw)=TF_n$，当$T\to \infty $时，$nw_0\rightarrow w$，因此
\begin{align}
X(jw)=\int_{-\infty}^{+\infty}f(t)e^{-jwt}\text{d}t
\end{align}
【注】这里为什么要记作$X(jw)$，主要是为了和傅里叶级数$F_n$相区别，$F_n$是离散谱线，而$X(jw)$是连续谱线。另外，傅里叶变换是拉普拉斯变换的特殊形式，即$s=\left( \sigma +j\omega \right)\left| _{\sigma =0} \right.$时，拉普拉斯变换就转换成了傅里叶变换。

傅里叶逆变换

\begin{align}
f(t)
&=\sum\limits_{n=-\infty}^{+\infty}F_ne^{jnw_0t}\\
&=\sum_{n=-\infty}^{+\infty}X(jw)\frac{1}{T}e^{jnw_0t}\\
&=\frac{1}{2\pi}\left(\sum_{n=-{\infty} }^{+\infty}X(jw)e^{jnw_0t}\right)\frac{2\pi}{T}
\end{align}
由于$T\to \infty $，因此$\frac{2\pi}{T}=w_o\to \text{d}w$（这里的$w_0$就是小柱条的宽），$w_0\to w$，由此前黎曼积分的知识，此时求和变成了积分
\begin{align}
f(t)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(jw)e^{jwt}\text{d}w
\end{align}
因此，信号$f(t)$的傅里叶变换对为
\begin{align}
f(t)&=\frac{1}{2\pi }\int_{-\infty }^{+\infty }X(jw ){ {e}^{jw t} }dw \\
X(jw )&=\int_{-\infty }^{+\infty }{f(t){ {e}^{-jw t} }dt} \\
\end{align}
至此，连续时间频域分析得到了统一，我们可以用频域分析法来分析信号。我们称傅里叶级数为频谱，称傅里叶变换为频谱密度，两者统称为频谱。

周期信号的傅里叶变换

一个周期为$T$的周期函数$f(t)$，可以展开成傅里叶级数
\begin{align}
f(t)=\sum_{n=-\infty}^{+\infty}F_ne^{-jnw_0t}
\end{align}
对两边取傅里叶变换
\begin{align}
\mathscr{F}[f(t)]=\mathscr{F}\left[\sum_{n=-\infty}^{+\infty}F_ne^{-jnw_0t} \right]=\sum_{n=-\infty}^{+\infty} F_n\mathscr{F}\left[e^{-jnw_0t}\right]
\end{align}
由于$\mathscr{F}\left[e^{-jnw_0t}\right]=2\pi \delta(w-w_0)$，因此
\begin{align}
\mathscr{F}[f(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_n\delta(w-w_0)
\end{align}