信号的正交分解

矢量的几何分解

为了理解对信号进行分解的目的，我们先从几何学的角度，回味下平面矢量以及空间矢量的分解。如图1所示，(a)$\overrightarrow{A}=c_1\overrightarrow{v_x}+c_2\overrightarrow{v_y}$，即将平面矢量分解成正交的$x$轴和$y$轴的单位矢量；（b）$\overrightarrow{A}=c_1\overrightarrow{v_x}+c_2\overrightarrow{v_y}+c_3\overrightarrow{v_z}$，即将空间矢量分解成正交的$x$轴、$y$轴和$z$轴的单位矢量。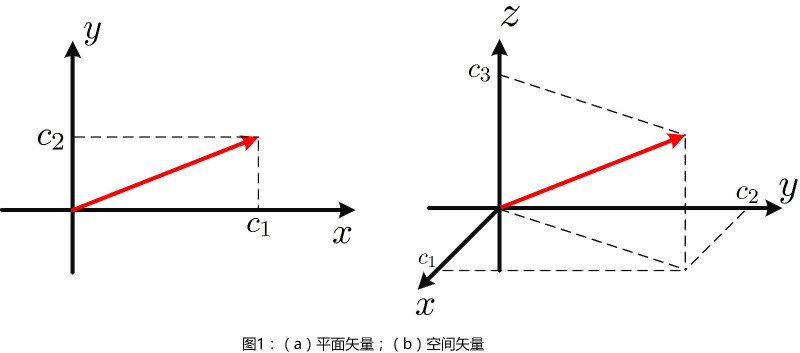

为此，我们先理清楚什么是矢量正交？

矢量正交的定义
若有$\overrightarrow{A}\cdot \overrightarrow{B}=0$，则矢量$\overrightarrow{A}$与$\overrightarrow{B}$正交。
为什么要对空间矢量进行正交分解？
很明显，方便分析！简化计算！为了方便理解，我们举一个高中牛顿力学的一个例子，如图2所示，固定斜面上有一小球，小球与斜面的接触面绝对光滑，现在要研究小球沿斜面的加速度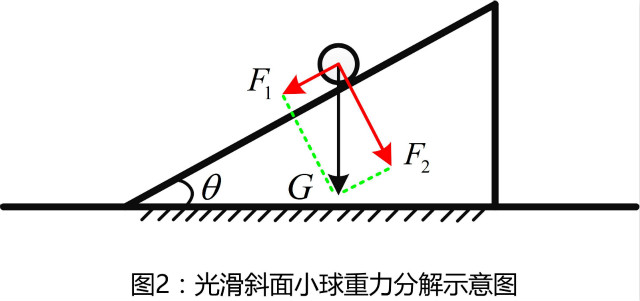

这样求得的斜面加速度为
\begin{align}
g=\sin \theta
\end{align}
可以看到通过矢量的正交分解，我们可以很轻松的求出小球沿斜面的加速度。将空间矢量正交分解的概念推广到信号空间，在信号空间中找到若干个相互正交的信号为基本信号，使得任意信号可以表示成这组正交的信号集合的线性组合。

正交信号

定义：在区间$(t_1,t_2)$上的两个信号$\phi_1(t)$和$\phi_2(t)$，若满足
\begin{align}
\int_{t_1}^{t_2}\phi_1(t)\phi_2(t)=0
\end{align}
则称$\phi_1(t)$和$\phi_2(t)$在区间$(t_1,t_2)$上正交。

正交函数集：如果有$n$个函数$\left\{\phi_1(t),\cdots,\phi_n(t)\right\}$构成一个函数集合，若函数集合在区间$(t_1,t_2)$上满足
\begin{align}
\int_{t_1}^{t_2}\phi_1(t)\phi_2(t)\text{d}t=\left\{
\begin{matrix}
0 &i\ne j\\
K &i=j
\end{matrix}
\right.
\end{align}
其中$K$为常数，则称此函数集为正交函数集。

完备正交函数集：定义集合$\mathcal{S}=\left\{\phi_1(t),\cdots,\phi_n(t)\right\}$是区间$(t_1,t_2)$上的正交函数集，如果除$\mathcal{S}$外，不存在函数$\phi(t)$满足等式
\begin{align}
\int_{t_1}^{t_2} \phi_i(t)\phi(t)=0\quad \forall i=\left\{1,\cdots,n\right\}
\end{align}
则称此函数集为完备正交函数集。我们称该完备集合中的函数$\phi_j(t)$为基或者基底。常见的完备正交函数集合有三角函数集、虚指数函数集。

Example: 证明三角函数集$\left\{1,\cos(nw_0t),\sin(nw_0t)\right\},(n=1,2,\cdots)$是正交函数集合
证：
\begin{align}
\int_{t_0}^{t_0+T}\cos(nw_0t)\cos(mw_0t)\text{d}t&=\left\{
\begin{matrix}
0 &m\ne n\\
\frac{T}{2} &m=n\ne 0\\
T &m=n=0
\end{matrix}
\right.\\
\int_{t_0}^{t_0+T}\sin(nw_0t)\sin(mw_0t)\text{d}t&=\left\{
\begin{matrix}
0 &m\ne n\\
\frac{T}{2} &m=n\ne 0
\end{matrix}
\right.\\
\int_{t_0}^{t_0+T}\sin(nw_0t)\cos(mw_0t)\text{d}t&=0
\end{align}
因此三角函数集为正交函数集。
【注】如果函数$f(t)$是周期为$T$的周期信号，则有$\int_{a}^{T+a}f(t)\text{d}t=\int_{0}^{T}f(t)\text{d}t$。

信号的正交分解

设$n$个函数$\phi_1(t),\cdots,\phi_n(t)$在区间$(t_1,t_2)$构成一个正交函数集$\mathcal{S}$。将任意信号$f(t)$表示成这$n$个函数的线性组合来近似，可表示为
\begin{align}
f(t)\approx a_1\phi_1(t)+\cdots a_n\phi_n(t)=\sum\limits_{i=1}^na_i\phi_i(t)
\end{align}
为此，我们需要确定$a_i (i=1,\cdots n)$的具体取值，来确保$\sum\limits_{i=1}^na_i\phi_i(t)$是对$f(t)$的最佳近似。我们选取均方误差（mean square error, MSE）来衡量这个近似的效果
\begin{align}
\text{MSE}=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}\left(f(t)-\sum\limits_{i=1}^na_i\phi_i(t)\right)^2\text{d}t
\end{align}
为使得MSE最小，计算MSE对$a_j$的偏导如下
\begin{align}
\frac{\partial \text{MSE} }{\partial a_j}
&=\frac{1}{t_2-t_1}\frac{\partial }{\partial a_j}\int_{t_1}^{t_2}\left(f(t)-\sum\limits_{i=1}^na_i\phi_i(t)\right)^2\text{d}t\\
&\overset{(a)}{=}\frac{1}{t_2-t_1}\int_{t_1}^{t_2}\frac{\partial }{\partial a_j}\left(f(t)-\sum\limits_{i=1}^na_i\phi_i(t)\right)^2\text{d}t\\
&=-\frac{1}{t_2-t_1}\int_{t_1}^{t_2}2\left(f(t)-\sum\limits_{i=1}^na_i\phi_i(t)\right)\phi_j(t)\text{d}t\\
&\overset{(b)}{=}\frac{2a_j}{t_2-t_1}\int_{t_1}^{t_2}\phi_j^2(t)\text{d}t-\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\phi_j(t)\text{d}t
\end{align}
其中步骤$(a)$成立，假设被积函数性质足够好，使得积分和偏导顺序可以交换；步骤$(b)$成立，利用完备正交函数集合，函数正交的性质。令偏导数为零，得到
\begin{align}
a_j=\frac{\int_{t_1}^{t_2}f(t)\phi_j(t)\text{d}t}{\int_{t_1}^{t_2}\phi_j^2(t)\text{d}t} \quad i=(1,\cdots,n)
\end{align}
定义$K_j=\int_{t_1}^{t_2}\phi_j^2(t)\text{d}t$，则参数$a_j$可以表示为
\begin{align}
a_j=\frac{1}{K_j}\int_{t_1}^{t_2}f(t)\phi_j(t)\text{d}t
\end{align}
到这里，我们会发现，信号的正交分解，跟矢量投影很相似。将矢量$\overrightarrow{A}$投影到矢量$\overrightarrow{a}$上，其投影长度$\frac{\overrightarrow{A}\cdot \overrightarrow{a} }{|\overrightarrow{a}|}$。注意这里所得到的$a_j$表达式是基于均方误差最小准则得到的，均方误差刻画的是真实值和近似值的欧式距离，根据不同的规则，可以得到不同的解。

连续时间傅里叶级数的三角级数形式

根据上一节知识，我们尝试将信号$f(t)$分解到三角函数集$\mathcal{S}=\left\{1,\cos(nw_0t),\sin(nw_0t)\right\},(n=1,\cdots)$上，即将$f(t)$表示成该集合中基的线性组合，如下
\begin{align}
f(t)=\frac{a_0}{2}+\sum\limits_{n=1}^{+\infty}a_n\cos(nw_0t)+\sum\limits_{n=1}^{+\infty}b_n\sin (nw_0t)
\end{align}
为了计算$a_n$

利用信号正交特性。利用信号正交特性，对等式两边同时乘上$\cos(nw_0t)$项，并在一个周期内进行积分，得到
\begin{align}
\int_T f(t)\cos(nw_0t)\text{d}t&=\int_T a_n\cos(nw_0t)\cos(nw_0t)\text{d}t\\
&=a_n\int _T\frac{1+\cos(2nw_0t)}{2}\text{d}t\\
&=\frac{a_nT}{2}
\end{align}
因此，得到
\begin{align}
a_n=\frac{2}{T}\int_T f(t)\cos(nw_0t)\text{d}t
\end{align}
同理，在等式两边乘上$\sin (nw_0t)$项，可以到$b_n$的表达式如下
\begin{align}
b_n=\frac{2}{T}\int_T f(t)\sin(nw_0t)\text{d}t
\end{align}
利用从均方误差最小得到的公式：$a_j=\frac{\int_{t_1}^{t_2}f(t)\phi_j(t)\text{d}t}{\int_{t_1}^{t_2}\phi_j^2(t)\text{d}t}$，来进行求解
\begin{align}
a_n&=\frac{\int_{t_1}^{t_2}f(t)\cos(nw_0t)\text{d}t}{\int \cos^2(nw_0t)\text{d}t}=\frac{2}{T}\int_Tf(t)\cos(nw_0t)\text{d}t\\
b_n&=\frac{\int_{t_1}^{t_2}f(t)\sin(nw_0t)\text{d}t}{\int \sin^2(nw_0t)\text{d}t}=\frac{2}{T}\int_Tf(t)\sin(nw_0t)\text{d}t\\
\end{align}
我们惊喜的发现：最佳近似估计的系数和傅里叶三角系数是相等的，也就是说傅里叶级数是一种对周期信号的最佳近似！

合并同频率的$\cos(nw_0t),\sin(nw_0t)$，如下
\begin{align}
f(t)=\frac{A_0}{2}+\sum\limits_{n=1}^{+\infty}A_n \cos(nw_0t+\psi_n)
\end{align}
其中
\begin{align}
\left\{
\begin{matrix}
A_0=a_0\qquad \quad \quad \quad\\
A_n=\sqrt{a_n^2+b_n^2}\quad \quad\\
\psi_n=-\arctan (\frac{b_n}{a_n})
\end{matrix}
\right.
\end{align}

连续时间傅里叶级数的虚指数形式

傅里叶级数是对周期信号的最佳近似，做这种近似的目的就是为了方便计算和分析信号，但是在实际信号分析中，使用三角级数计算比较麻烦。因此通过欧拉公式将傅里叶级数的三角形式转换成指数形式。
\begin{align}
\cos(t)=\frac{e^{jt}+e^{-jt} }{2}
\end{align}
应用欧拉公式，信号$f(t)$表示为
\begin{align}
f(t)&=\frac{A_0}{2}+\sum\limits_{n=1}^{+\infty}\frac{A_n}{2}\left(e^{j(nw_0t+\psi_n)}+e^{-j(nw_0t+\psi_n)}\right)\\
&=\frac{A_0}{2}+\sum\limits_{n=1}^{+\infty}\frac{A_n}{2}e^{j(nw_0t+\psi_n)}+\sum\limits_{n=1}^{+\infty}\frac{A_n}{2}e^{-j(nw_0t+\psi_n)}\\
&=\frac{A_0}{2}+\sum\limits_{n=1}^{+\infty}\frac{A_n}{2}e^{j(nw_0t+\psi_n)}+\sum\limits_{n=-1}^{-\infty}\frac{A_{-n} }{2}e^{jnw_0t}e^{-j\psi_{-n} }
\end{align}
由于$A_n=\sqrt{a_n^2+b_n^2}$是关于$n$的偶函数，$\psi_n$是关于$n$的奇函数，因此有
\begin{align}
f(t)=\frac{A_0}{2}+\sum\limits_{n=1}^{+\infty}\frac{A_n}{2}e^{j(nw_0t+\psi_n)}+\sum\limits_{n=-1}^{-\infty}\frac{A_n}{2}e^{j(nw_0t+\psi_n)}
\end{align}
令$A_n|_{n=0}=A_0$，因此有
\begin{align}
f(t)=\sum\limits_{n=-\infty}^{+\infty}\frac{A_n}{2}e^{j\psi_n}e^{jnw_0t}
\end{align}
令$F_n=\frac{A_n}{2}e^{j\psi_n}$，即得到信号的傅里叶级数的虚指数形式的表达式
\begin{align}
f(t)=\sum\limits_{n=-\infty}^{+\infty}F_ne^{jnw_0t}
\end{align}
类似地，这里$F_n$的表达式也可以利用信号正交或者均方误差最小的方式来求解，得到
\begin{align}
F_n=\frac{1}{T}\int_T f(t)e^{-jnw_0t}\text{d}t
\end{align}