Notations:

$\text{Diag}(\boldsymbol{x})$表示以矢量为矩阵对角线元素构成对角阵，如$\text{Diag}(a,b)=\left({
\begin{array}{cccc}
a&0
\\0&b
\end{array}
}\right)$；

粗体符号表示矩阵或者矢量，如$\boldsymbol{x}$表示矢量，$\boldsymbol{A}$表示矩阵。

#特征值与特征向量
矩阵的乘法对应着一种线性变换使得原向量在方向和长度上发生变化，比如$f(\boldsymbol{x})=\boldsymbol{A}\boldsymbol{x}\quad (\boldsymbol{x}\in \mathbb{R}^n, \boldsymbol{A}\in \mathbb{R}^{m\times n})$，$f$表示从$\mathbb{R}^n$空间到$\mathbb{R}^m$空间的一种线性映射关系。我们考虑$\boldsymbol{A}$是方阵的情况。
\begin{align}
\boldsymbol{y}=\boldsymbol{Ax}
\end{align}
其中$\boldsymbol{y}\in \mathbb{R}^m$。矩阵$\boldsymbol{A}$与向量$\boldsymbol{x}$相乘，表示对$\boldsymbol{x}$进行一次方向和长度上的变换，即向量$\boldsymbol{y}$。
例如：$\boldsymbol{A}=\left({\begin{array}{cccc}a_{11},a_{12}\\a_{21},a_{22}\end{array} }\right)$, $\boldsymbol{x}=(b_1,b_2)^\text{T}$，则
\begin{align}
\boldsymbol{y}=\left({
\begin{array}{cccc}
a_{11}b_1+a_{12}b_2\\
a_{21}b_1+a_{22}b_2
\end{array}
}\right)
\end{align}
$|\boldsymbol{x}|=\sqrt{b_1^2+b_2^2},\ |\boldsymbol{y}|=\sqrt{(a_{11}b_1+a_{12}b_2)^2+(a_{21}b_1+a_{22}b_2)^2}$
$\angle(\boldsymbol{x},\boldsymbol{y})=\cos^{-1}\frac{b_1(a_{11}b_1+a_{12}b_2)+b_2(a_{21}b_1+a_{22}b_2)}{|\boldsymbol{x}||\boldsymbol{y}|}$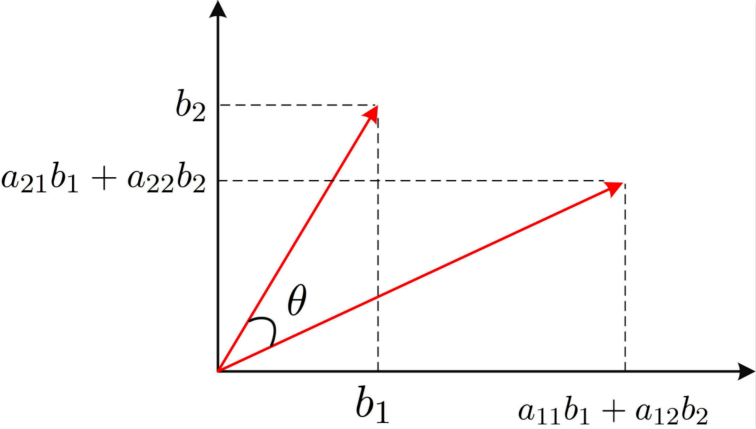
Text
问题：对于线性变换矩阵$\boldsymbol{A}$,是否存在这样一个向量$\boldsymbol{\xi}$, 经过这种特定的变换之后保持方向不变，只是进行长度上的拉伸，即使得$\angle (\boldsymbol{\xi},\boldsymbol{y})=0,\ |\boldsymbol{y}|=|\lambda| |\boldsymbol{\xi}|$。

定义：设$\boldsymbol{A}$是$n$阶方阵，如果数$\lambda$和$n$维非零列向量$\boldsymbol{x}$满足
\begin{align}
\boldsymbol{Ax}=\lambda\boldsymbol{x}
\end{align}
称$\lambda$是矩阵$\boldsymbol{A}$的特征值，$\boldsymbol{x}$是矩阵$\boldsymbol{A}$对应$\lambda$的特征向量[1]。

根据上面的描述，我们知道，特征向量就是这样一个满足经过线性变换阵$\boldsymbol{A}$之后，只发生长度上变换，方向不变的向量。那我们为什么求这样的特征值与特征向量呢？可以这样理解，对于一个实际的线性系统，其特性可以用矩阵$\boldsymbol{A}$来描述，对于输入向量$\boldsymbol{x}$，系统输出为$\boldsymbol{y}$会出现相位滞后、放大或者缩小等现象，而对于输入为特征向量$\xi$，该系统的输出只发生缩放，没有相位的变化。

设$\boldsymbol{\xi}_i$是矩阵对应于$\lambda_i$的特征值，则有
\begin{align}
&\boldsymbol{A\xi}_i=\lambda_i\boldsymbol{\xi}_i\\
&\Rightarrow (\boldsymbol{A\xi}_1,\cdots,\boldsymbol{A\xi}_n)=(\lambda_1\boldsymbol{\xi}_1,\cdots,\lambda_n\boldsymbol{\xi}_n)\\
&\Rightarrow \boldsymbol{A}(\boldsymbol{\xi}_1,\cdots,\boldsymbol{\xi}_n)=(\boldsymbol{\xi}_1,\cdots,\boldsymbol{\xi}_n)\left({
\begin{array}{cccc}
\lambda_1& & & \\
&\lambda_2 & &\\
& &\ddots &\\
& & &\lambda_n
\end{array}
}\right)
\end{align}
令$\boldsymbol{P}=(\boldsymbol{\xi}_1,\cdots,\boldsymbol{\xi}_n)$，$\boldsymbol{\Lambda}=\text{Diag}(\lambda_1,\cdots,\lambda_n)$则有
\begin{align}
\boldsymbol{AP}=\boldsymbol{P}\boldsymbol{\Lambda}
\end{align}
因此，矩阵$\boldsymbol{A}$对角化的问题就等价于方阵$\boldsymbol{P}$是否可逆，即$\boldsymbol{A}$是否有$n$个线性无关的特征向量。矩阵$\boldsymbol{A}$有$n$个线性无关的特征向量有两种情况

$n$阶方阵$\boldsymbol{A}$有$n$个不同的特征值，对应有$n$线性无关的特征向量。

$n$阶方阵$\boldsymbol{A}$有重根情况，且对应$k$重根特征值$\lambda$，有$n-\text{rank}(\boldsymbol{A}-\lambda\mathbf{I})=k$。

注意，并不是任意的矩阵都可以相似对角化。以下针对$\boldsymbol{P}$可逆的情况，那么有
\begin{align}
\boldsymbol{A}=\boldsymbol{P\Lambda P}^{-1}
\end{align}
进一步的，若$\boldsymbol{P}$是一个正交矩阵，即
\begin{align}
\boldsymbol{A}=\boldsymbol{P\Lambda P}^{T}=\sum\limits_{i=1}^n\lambda_i\boldsymbol{\xi}_i\boldsymbol{\xi}^\text{T}
\end{align}也就是说，$\boldsymbol{A}$矩阵可以由特征向量线性组合进行表示。

奇异值分解

矩阵的特征值分解仅仅是针对方阵的，对于长方形矩阵$\boldsymbol{A}\in \mathbb{R}^{m\times n}$，也存在着类似的分解，称奇异值分解[2]。
定义：设矩阵$\boldsymbol{A}\in \mathbb{R}^{m\times n}$，且$rank(\boldsymbol{A})=r$，则存在$m$阶正交矩阵$\boldsymbol{V}$和$n$阶正交矩阵$\boldsymbol{U}$，使得
\begin{align}
\boldsymbol{A}=\boldsymbol{V\Sigma U}^\text{T}
\end{align}
其中$\boldsymbol{\Sigma}=\left({
\begin{array}{cccc}
\boldsymbol{\Lambda} &\boldsymbol{0}_{(r)\times(n-r)}\\
\boldsymbol{0}_{(m-r)\times r} &\boldsymbol{0}_{(m-r)\times(n-r)}
\end{array} }\right)$，其中$\boldsymbol{\Lambda}=\text{Diag}(\sigma_1,\sigma_2,\cdots,\sigma_r)$，并且$\sigma_1\geq\sigma_2\cdots\geq\sigma_r\geq 0$。
证：因为$\text{rank}(\boldsymbol{A})=r$，因此设$\boldsymbol{A}^\text{T}\boldsymbol{A}$的特征值为
\begin{align}
\sigma_1^2\geq\cdots,\geq \sigma_r^2\geq0,\quad \sigma_{r+1}^2=\sigma_{n}^2=0
\end{align}
由于$\boldsymbol{A}^\text{T}\boldsymbol{A}$是对称矩阵，因此必可以相似对角化[1]，即存在正交矩阵$U$，使得
\begin{align}
\boldsymbol{U}^\text{T}\boldsymbol{A}^\text{T}\boldsymbol{A}\boldsymbol{U}=\text{Diag}(\sigma_1^2,\cdots,\sigma_r^2,\underbrace{0,\cdots,0}_{n-r})
\end{align}
记$\boldsymbol{U}=[\boldsymbol{U}_1,\boldsymbol{U}_2]$,其中$\boldsymbol{U}_1$是一个$n\times r$的矩阵，$\boldsymbol{U}_2$是一个$n\times(n-r)$的矩阵。因此，上式可以写为
\begin{align}
\boldsymbol{A}^\text{T}\boldsymbol{A}[\boldsymbol{U}_1,\boldsymbol{U}_2]=[\boldsymbol{U}_1,\boldsymbol{U}_2]\left({
\begin{array}{cccc}
\boldsymbol{\Lambda}^2 &\boldsymbol{0}\\
\boldsymbol{0} &\boldsymbol{0}
\end{array}
}\right)
\end{align}
则有
\begin{align}
\boldsymbol{A}^\text{T}\boldsymbol{AU}_1=\boldsymbol{U}_1\boldsymbol{\Lambda}^2,\quad \boldsymbol{A}^\text{T}\boldsymbol{AU}_2=\boldsymbol{0}
\end{align}
记$\boldsymbol{V}=[\boldsymbol{V}_1,\boldsymbol{V}_2]$，其中$\boldsymbol{V}_1$是$m\times r$矩阵，$\boldsymbol{V}_2$是$m\times(m-r)$矩阵
\begin{align}
\boldsymbol{A}^\text{T}\boldsymbol{AU}_1=\boldsymbol{U}_1\boldsymbol{\Lambda}^2\ \Rightarrow \boldsymbol{A}^\text{T}\boldsymbol{AU}_1\boldsymbol{\Lambda}=\boldsymbol{U}_1\boldsymbol{\Lambda}
\end{align}
令$\boldsymbol{V}_1=\boldsymbol{AU}_1\boldsymbol{\Lambda}^{-1}$，有
\begin{align}
\boldsymbol{V}_1^\text{T}\boldsymbol{V}_1&=(\boldsymbol{AU}_1\boldsymbol{\Lambda}^{-1})^\text{T}\boldsymbol{AU}_1\boldsymbol{\Lambda}^{-1}\\
&=\boldsymbol{\Sigma}^{-1}\boldsymbol{U}_1^\text{T}\boldsymbol{A}^\text{T}\boldsymbol{A}\boldsymbol{U}_1\boldsymbol{\Sigma}^{-1}\\
&=\boldsymbol{\Lambda}^{-1}\boldsymbol{\Sigma}^2\boldsymbol{\Lambda}^{-1}\\
&=\mathbf{I}_{r}
\end{align}
即$\boldsymbol{V}_1$是列正交规范化矩阵。取$\boldsymbol{V}_2$，使得$\boldsymbol{V}=[\boldsymbol{V}_1,\boldsymbol{V}_2]$是正交矩阵，因此
\begin{align}
\boldsymbol{V}_2\boldsymbol{\boldsymbol{AU}_1}=\boldsymbol{V}_2^\text{T}\boldsymbol{V}_1\boldsymbol{\Lambda}=\boldsymbol{0}
\end{align}
那么
\begin{align}
\boldsymbol{V}^\text{T}\boldsymbol{A}\boldsymbol{U}=
\left({
\begin{array}{cccc}
\boldsymbol{V}_1^\text{T}\\
\boldsymbol{V}_2^\text{T}
\end{array}
}\right)\boldsymbol{A}[\boldsymbol{U}_1,\boldsymbol{U}_2]=
\left({
\begin{array}{cccc}
\boldsymbol{V}_1^\text{T}\boldsymbol{A}\boldsymbol{U}_1 &\boldsymbol{V}_1^\text{T}\boldsymbol{A}\boldsymbol{U}_2\\
\boldsymbol{V}_2\boldsymbol{AU}_1,&\boldsymbol{V}_2^\text{T}\boldsymbol{AU}_2
\end{array}
}\right)=\left({
\begin{array}{cccc}
\boldsymbol{\Lambda} &\boldsymbol{0}\\
\boldsymbol{0} &\boldsymbol{0}
\end{array}
}\right)
\end{align}
即
\begin{align}
\boldsymbol{A}=\boldsymbol{V}\boldsymbol{\Sigma}\boldsymbol{U}^\text{T}
\end{align}

Pseudo逆矩阵

令$\boldsymbol{A}=\boldsymbol{V\Sigma U}^\text{T}$是矩阵$\boldsymbol{A}\in \mathbb{R}^{m\times n}$的奇异值分解，且$\text{rank}(\boldsymbol{A})=r$，定义矩阵$\boldsymbol{A}$的pseudo逆为
\begin{align}
\boldsymbol{A}^{+}=\boldsymbol{U}\boldsymbol{\Sigma}^{-1}\boldsymbol{V}^\text{T}\in \mathbb{R}^{n\times m}
\end{align}
也称为Moore-Penrose广义逆矩阵。另外一种表达式是
\begin{align}
\boldsymbol{A}^{+}=(\boldsymbol{A}^\text{T}\boldsymbol{A})^{-1}\boldsymbol{A}^\text{T}=\boldsymbol{A}^\text{T}(\boldsymbol{AA}^\text{T})^{-1}
\end{align}
可以很容易证明两种表达式是等价的，我们可以从长方形矩阵的奇异分解来解释第二个式子表达式的合理性。当$m>n$时，采用$\boldsymbol{A}^{+}=(\boldsymbol{A}^\text{T}\boldsymbol{A})^{-1}\boldsymbol{A}^\text{T}$；当$m<n$时，通常采用$\boldsymbol{A}^{+}=\boldsymbol{A}^\text{T}(\boldsymbol{AA}^\text{T})^{-1}$。

References
[1] 同济大学数学系, 线性代数[M].北京: 高等教育出版社, 2012.
[2] 戴华, 矩阵论[M].北京: 科学出版社, 2015.